기본 코드는 파이토치 공식 튜토리얼 코드를 이용하였으며, 약간의 코드를 덧붙였습니다.
전체 코드 :
사용된 데이터 : download.pytorch.org/tutorial/hymenoptera_data.zip
파일 및 폴더 구성 :
./classification_resnet.ipynb
./data/hymenoptera_data/train
./data/hymenoptera_data/val
위 형태가 되도록 폴더 구성을 해 주시면 됩니다.
불러올거 불러오기
# License: BSD
# Author: Sasank Chilamkurthy
# https://tutorials.pytorch.kr/beginner/transfer_learning_tutorial.html
# https://pytorch.org/docs/stable/torchvision/models.html
from __future__ import print_function, division
import torch
import torch.nn as nn
import torch.optim as optim
from torch.optim import lr_scheduler
import numpy as np
import torchvision
from torchvision import datasets, models, transforms
import matplotlib.pyplot as plt
import time
import os
import copy
plt.ion() # 대화형 모드
데이터 세팅
data_transforms = {
'train': transforms.Compose([
transforms.RandomResizedCrop(224),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
]),
'val': transforms.Compose([
transforms.Resize(256),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
]),
}
data_dir = 'data/hymenoptera_data'
image_datasets = {x: datasets.ImageFolder(os.path.join(data_dir, x),
data_transforms[x])
for x in ['train', 'val']}
dataloaders = {x: torch.utils.data.DataLoader(image_datasets[x], batch_size=16,
shuffle=True, num_workers=4)
for x in ['train', 'val']}
dataset_sizes = {x: len(image_datasets[x]) for x in ['train', 'val']}
class_names = image_datasets['train'].classes
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
이미지를 보여주기 위해 전처리 된 텐서 이미지를 원본 이미지로 복구하는 함수
(data_transforms 에서 normalize 한 것의 역산)
def imshow(inp, title=None):
"""Imshow for Tensor."""
inp = inp.numpy().transpose((1, 2, 0))
mean = np.array([0.485, 0.456, 0.406])
std = np.array([0.229, 0.224, 0.225])
inp = std * inp + mean
inp = np.clip(inp, 0, 1)
plt.imshow(inp)
if title is not None:
plt.title(title)
plt.pause(0.001) # 갱신이 될 때까지 잠시 기다립니다.
이미지 보여주기
# 학습 데이터의 배치를 얻습니다.
inputs, classes = next(iter(dataloaders['train']))
# 배치로부터 격자 형태의 이미지를 만듭니다.
out = torchvision.utils.make_grid(inputs)
imshow(out, title=[class_names[x] for x in classes])
학습부분 정의
def train_model(model, criterion, optimizer, scheduler, num_epochs=25):
since = time.time()
best_model_wts = copy.deepcopy(model.state_dict())
best_acc = 0.0
for epoch in range(num_epochs):
print('Epoch {}/{}'.format(epoch, num_epochs - 1))
print('-' * 10)
# 각 에폭(epoch)은 학습 단계와 검증 단계를 갖습니다.
for phase in ['train', 'val']:
if phase == 'train':
model.train() # 모델을 학습 모드로 설정
else:
model.eval() # 모델을 평가 모드로 설정
running_loss = 0.0
running_corrects = 0
# 데이터를 반복
for inputs, labels in dataloaders[phase]:
inputs = inputs.to(device)
labels = labels.to(device)
# 매개변수 경사도를 0으로 설정
optimizer.zero_grad()
# 순전파
# 학습 시에만 연산 기록을 추적
with torch.set_grad_enabled(phase == 'train'):
outputs = model(inputs)
_, preds = torch.max(outputs, 1)
loss = criterion(outputs, labels)
# 학습 단계인 경우 역전파 + 최적화
if phase == 'train':
loss.backward()
optimizer.step()
# 통계
running_loss += loss.item() * inputs.size(0)
running_corrects += torch.sum(preds == labels.data)
if phase == 'train':
scheduler.step()
epoch_loss = running_loss / dataset_sizes[phase]
epoch_acc = running_corrects.double() / dataset_sizes[phase]
print('{} Loss: {:.4f} Acc: {:.4f}'.format(
phase, epoch_loss, epoch_acc))
# 모델을 깊은 복사(deep copy)함
if phase == 'val' and epoch_acc > best_acc:
best_acc = epoch_acc
best_model_wts = copy.deepcopy(model.state_dict())
print()
time_elapsed = time.time() - since
print('Training complete in {:.0f}m {:.0f}s'.format(
time_elapsed // 60, time_elapsed % 60))
print('Best val Acc: {:4f}'.format(best_acc))
# 가장 나은 모델 가중치를 불러옴
model.load_state_dict(best_model_wts)
return model
시각화 함수
def visualize_model(model, num_images=6):
was_training = model.training
model.eval()
images_so_far = 0
fig = plt.figure()
with torch.no_grad():
for i, (inputs, labels) in enumerate(dataloaders['val']):
inputs = inputs.to(device)
labels = labels.to(device)
outputs = model(inputs)
_, preds = torch.max(outputs, 1)
for j in range(inputs.size()[0]):
images_so_far += 1
ax = plt.subplot(num_images//2, 2, images_so_far)
ax.axis('off')
ax.set_title('predicted: {}'.format(class_names[preds[j]]))
imshow(inputs.cpu().data[j])
if images_so_far == num_images:
model.train(mode=was_training)
return
model.train(mode=was_training)- 예측한 이미지와 예측한 내용을 같이 보여줄 함수
모델 파라미터 세팅
#model_ft = models.resnet18(pretrained=True)
model_ft=models.resnet18(pretrained=True)
num_ftrs = model_ft.fc.in_features
# 여기서 각 출력 샘플의 크기는 2로 설정합니다.
# 또는, nn.Linear(num_ftrs, len (class_names))로 일반화할 수 있습니다.
model_ft.fc = nn.Linear(num_ftrs, 2)
model_ft = model_ft.to(device)
criterion = nn.CrossEntropyLoss()
# 모든 매개변수들이 최적화되었는지 관찰
optimizer_ft = optim.SGD(model_ft.parameters(), lr=0.001, momentum=0.9)
# 7 에폭마다 0.1씩 학습율 감소
exp_lr_scheduler = lr_scheduler.StepLR(optimizer_ft, step_size=7, gamma=0.1)
실제 트레이닝 시작
model_ft = train_model(model_ft, criterion, optimizer_ft, exp_lr_scheduler,
num_epochs=25)- num_epochs 줄 바꾼건 이리저리 바꾸는거 테스트 해 보느라...

예측을 어떻게 했는지 보자
visualize_model(model_ft)
자, 이번엔 cnn 부분의 weight를 그대로 활용해서(변경하지 않고) fnn 부분만 학습시켜보자.
(시신경은 놔두고, 구분하는 로직만 변경했을 때 어떻게 되는지 보자!)
#model_conv = torchvision.models.resnet18(pretrained=True)
model_conv = torchvision.models.resnet18(pretrained=True)
for param in model_conv.parameters():
param.requires_grad = False
# 새로 생성된 모듈의 매개변수는 기본값이 requires_grad=True 임
num_ftrs = model_conv.fc.in_features
model_conv.fc = nn.Linear(num_ftrs, 2)
model_conv = model_conv.to(device)
criterion = nn.CrossEntropyLoss()
# 이전과는 다르게 마지막 계층의 매개변수들만 최적화되는지 관찰
optimizer_conv = optim.SGD(model_conv.fc.parameters(), lr=0.001, momentum=0.9)
# 7 에폭마다 0.1씩 학습율 감소
exp_lr_scheduler = lr_scheduler.StepLR(optimizer_conv, step_size=7, gamma=0.1)- 위랑 비슷할텐데 for 구분이 추가되었다. 불러온 resnet18의 requires_grad를 꺼버린다는건데, 기존에 학습된 가중치를 그대로 쓰겠다고 보면 된다.
- 나머지 조건은 동일
model_conv = train_model(model_conv, criterion, optimizer_conv,
exp_lr_scheduler, num_epochs=25)
정확도가 올랐다!
94.7712% -> 95.4248%
0.6536% 올랐다!
튜토리얼 끝
저장은 이렇게 하면 됨
torch.save({
'model_state_dict': model_conv.state_dict(),
'optimizer_state_dict': optimizer_conv.state_dict(),
'loss': criterion
}, 'd:/test.pt')
기존 모델 파라미터도 같이 바꿔보면 어떨까?
for param in model_conv.parameters():
param.requires_grad = True
model_conv = train_model(model_conv, criterion, optimizer_conv,
exp_lr_scheduler, num_epochs=25)
- 아쉽게도 안올랐다. 오르는 경우가 있을수도 있다만... 이 경우에는 시신경쪽까지 바꾸는 대공사를 해도 별 의미가 없었다. 기존에 학습해둔 resnet 18의 시신경이 워낙 우수해서 기존 신경망으로도 별/개미 정도 구분하는데 지장없을 정도였다 정도로 보면 될 것 같다. (막상 Epoch 수가 늘어나거나 다른 파라미터가 바뀌면 또 다를 수 있다.)
모델 학습부분 끝
여기부터는 모델의 예측에 대한 정밀도의 비례성을 알아보기 위한 추가 부분
기본적으로 우리 모델에서는 확률값 중 높은 녀석을 예측하게 되어있다.
우선 여기서부터는 개미는 잊도록 하자. 이 모델은 사진에 '벌이 있는지 없는지'를 구분하는 모델이다. (제가 그렇게 정했어요.)
벌이 있는 것 같을 때 사람들은 '50% 확률로 정도 벌이 있을 것 같은데...?' 라고 생각하거나 '90%정도 확률로 벌이 있을 것 같은데...?'라고 생각할 수 있다.
딥러닝 모델도 그럴 수 있다.
저 사람이 말하면 일단 믿고봐도 될 사람(실수가 적은, 확실할 때만 말하는)일까? 라는 기준으로 한 번 생각해보자.
(민감하고 예민한 사람인지는 아래 부분의 Precision을 recall 으로 바꿔서 처리하면 된다.)
근데 진짜로 그럴까? 저 사람(모델)이 확률이 높다고 하면 실제로 더 신빙성 있을까?
그럴 것 같은데... 확인해보자.
결과물을 빼내기 위한 함수 설정
def result_out(model, num_images=6):
was_training = model.training
model.eval()
images_so_far = 0
fig = plt.figure()
# added
temp = {}
temp['inputs'] = []
temp['labels'] = []
temp['outputs'] = []
temp['preds'] = []
with torch.no_grad():
for i, (inputs, labels) in enumerate(dataloaders['val']):
inputs = inputs.to(device)
labels = labels.to(device)
outputs = model(inputs)
temp['inputs'].append(inputs)
temp['labels'].append(labels)
temp['outputs'].append(outputs)
_, preds = torch.max(outputs, 1)
temp['preds'].append(preds)
model.train(mode=was_training)
return temp- input/labels/output을 세트로 함수 바깥으로 빼내는 함수
위 함수의 결과값을 받아서 변수에 넣음
result_fin = result_out(model_conv)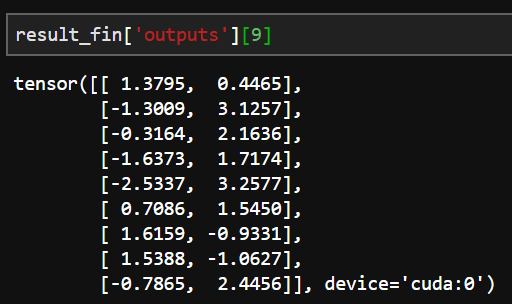

리턴 받은 내용 확인
result_fin['preds']
나라시평탄화를 하자
labels = []
for i in range(len(result_fin['labels'])):
for j in range(len(result_fin['labels'][i])):
labels.append(int(result_fin['labels'][i][j]))
outputs = []
for i in range(len(result_fin['outputs'])):
for j in range(len(result_fin['outputs'][i])):
outputs.append(list(result_fin['outputs'][i][j]))
preds = []
for i in range(len(result_fin['preds'])):
for j in range(len(result_fin['preds'][i])):
preds.append(int(result_fin['preds'][i][j]))
파이썬 데이터 분석의 필수품 pandas 소환해서 df로 전환하고 확인
import pandas as pd
df_outputs = pd.DataFrame(outputs)
df_outputs
전처리 해 줘야지 별 수 있나..
# 각각 float으로 바꿔서 넣음
outputs = []
for i in range(len(result_fin['outputs'])):
for j in range(len(result_fin['outputs'][i])):
#outputs.append(list(result_fin['outputs'][i][j]))
outputs.append(
[ float(result_fin['outputs'][i][j][0]) , float(result_fin['outputs'][i][j][1]) ]
)
outputs[:5]

이쁘게 DataFrame 옷을 입혀주자
df_outputs = pd.DataFrame(outputs)
df_outputs
좀 더 직관적인 확률로 전환하기 위해 정규화를 해 주자. 저 대로면 어디서 끊어야 90% 확률인지 알기가 힘들다.
# 최대값
max_for_n = max(max(df_outputs[0]),max(df_outputs[1]))
max_for_n4.535218238830566 (그냥 타이핑 하고싶어서 복붙 안하고 직접 적었다.)
# 최솟값
min_for_n = min(min(df_outputs[0]),min(df_outputs[1]))
min_for_n-3.406691551208496 (이건 음수라서 복붙했다.)
정규화 하고 이쁜 DataFrame 옷까지 입혀주자. 분명히 pandas로 쉽게 하는 방법이 있을텐데 찾아보기 귀찮아서 그냥 이렇게 했다. 기억력이 좋았으면 나도 pandas로 했을거다. 근데 보고 따라오는 사람한테는 이게 더 나을수도 있을 것 같다.
df_output_mutate = [[],[]]
df_output_mutate[0] = []
df_output_mutate[1] = []
for (x,y) in zip(df_outputs[0],df_outputs[1]) :
temp0 = (x-min_for_n)/(max_for_n-min_for_n)
temp1 = (y-min_for_n)/(max_for_n-min_for_n)
df_output_mutate[0].append(temp0)
df_output_mutate[1].append(temp1)
df_output_mutate = pd.DataFrame(df_output_mutate)
df_output_mutate = df_output_mutate.T
df_output_mutate
데이터 분석의 친구 matplotlib친구 소환! 확률값들의 분포를 그려줘!
import matplotlib.pyplot as plt
plt.hist(output_ex)- 남들은 차트 이쁘게 꾸미던데... 난 그런 센스 없으니 그냥 심플하게 그린다.

이제 좀 확률값 답게 최소 0 최대1으로 이쁘게 정리가 되었다.
히스토그램을 왜 그렸냐고 물어본다면 저건 그냥 습관이다. 데이터를 다룬다면 값 분포 확인은 그냥 본능이어야 한다. (리신 Q 맞추면 뒷일은 날아가는 동안에 생각해야 하는 것 처럼)
혹시 모르니 값이 이쁘게 나왔는지 다시 확인한다.
df_output_mutate[:][:10]
벌이 아닐 확률 + 벌일 확률은?
df_output_mutate[0][1]+df_output_mutate[1][1]1.0641538788159415
????????????????????????
1이 안나온다.

어쩌겠어... 벌이아닐확률 + 벌일확률 = 1이 되도록 바꿔줘야지.
단, b만 궁금하니까 b/(a+b) 에 넣으면 되겠다.
a/(a+b) + b/(a+b) = 1 이니까 b/(a+b)만 가져다 쓰는겁니다.
output_for_pred = []
for i in range(len(df_output_mutate)):
temp = df_output_mutate[1][i]/(df_output_mutate[0][i]+df_output_mutate[1][i])
output_for_pred.append(temp)
output_for_pred[:10]

임계치별 정밀도를 구하는 함수를 만들어 보자.
def cal_precision(threashold,labels, preds):
TP = 0
FP = 0
same = 0
if len(labels) == len(preds):
for i in range(len(labels)):
if (labels[i] == 1) and (preds[i] == 1): # 실제 양성 / 예측 양성 = True Positive
TP = TP +1
elif (labels[i] == 0) and (preds[i] == 1): # 실제 음성 / 예측 양성 = False Positive
FP = FP +1
if labels[i] == preds[i]:
same = same +1
else:
print("error")
return 0
try:
PRE = TP/(TP+FP)
return [threashold,TP,FP,PRE,same,same/len(labels)]
except:
return [threashold,TP,FP,0,same,same/len(labels)]- 참 쉽죠? True positive, False positive만 세어주면 됩니다. 서비스로 accuracy도 넣었는데... 굳이 필요는 없어요.
임계치를 조금씩 바꿔가며 확인할 함수를 만듭니다.(굳이 함수 안만들어도 되는데 보기 편하려고 만들었어요.)
def cal_precision_full(labels, output_for_pred):
temp_res = []
for i in list(range(1,100000)):
temp_pred = [ 1 if x > i*0.00001 else 0 for x in output_for_pred]
temp_res.append(cal_precision(i*0.001,labels,temp_pred))
return temp_res이쁘게 만들자 마자 이쁘게 꾸며줍시다.
df_final = pd.DataFrame(cal_precision_full(labels, output_for_pred))
df_final.columns = ["Threashold","TP","FP","Precision","Correct","Accuracy"]
df_final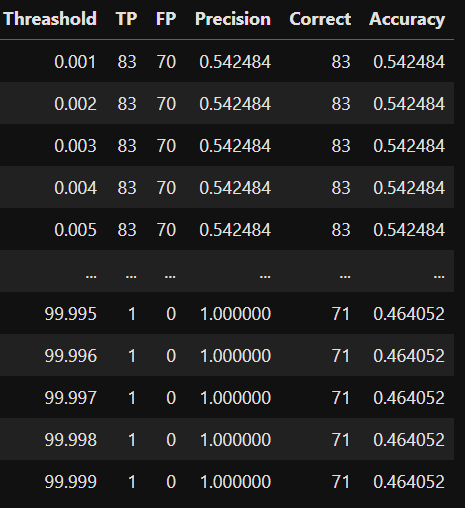
Precision이 어느순간부터인가 1을 찍고있는게 보일겁니다. 언제부터지?
대충 산점도 그리는 코드
f1 = plt.figure(figsize=(12,12))
plt.plot('Threashold','Precision', data=df_final,
linestyle='none', marker='o', markersize=2,color='blue',alpha=0.01
)
plt.plot([66,66],[0.5,1], color='red', lw=1, linestyle='solid')
plt.title('Scatter Plot of Precision', fontsize=20)
plt.xlabel('Threashold', fontsize=14)
plt.ylabel('Precision', fontsize=14)
plt.show()

대충 보니까 임계치 65930+1 부터 65939 번째 사이에는 있을 것 같다.

대충 임계치 65.935% 이상부터는 정밀도가 100%라는 의미일텐데...

이 예측값을 활용해서 임계치를 65.935 이상으로 잡으면 벌을 놓치긴 하겠지만 벌 없는 걸 보고 벌 있다고는 안하는 '믿음직한' 모델이 될거다.
말을 많이 하면 신뢰도가 떨어진다고들 하는데, 결국 더 확실할 때 이야기 하면 한 번 한번의 신뢰도가 높아지기 때문이다. 사회 생활에서 아주 의미있는 단어이기도 하지만 이런 모델이 중요한 상황들도 있으리라 생각한다.
다시... 제목으로 돌아와서. 제목이 왜 저러냐면

산점도를 보면 임계치가 올라가는데 정밀도는 떨어지는 구간들이 있다.
전반적으로 임계치가 올라가면(모델이 확신하는 정도가 올라가면) 정밀도도 증가하지만, 모델이 뱉은 output의 정확도를 신뢰하기 힘든 구간들이 분명히 존재한다는 뜻이다.

0.984848 -> 0.984127 -> 0.982759 -> 0.981818
임계치를 높임에도 불구하고 Precision이 떨어지는 것을 확인할 수 있다.
확률 합계를 1로 맞춰주는 과정에서 비율의 문제로 이런 현상이 생겼는지 테스트 하기 위해 b/(a+b)를 하기 전 데이터로 다시 확인 해 보자
df_final2 = pd.DataFrame(cal_precision_full(labels, df_output_mutate[1]))
df_final2.columns = ["Threashold","TP","FP","Precision","Correct","Accuracy"]
df_final2f1 = plt.figure(figsize=(12,12))
plt.plot('Threashold','Precision', data=df_final2,
linestyle='none', marker='o', markersize=2,color='blue',alpha=0.01
)
plt.plot([66,66],[0.5,1], color='red', lw=1, linestyle='solid')
plt.title('Scatter Plot of Precision', fontsize=20)
plt.xlabel('Threashold', fontsize=14)
plt.ylabel('Precision', fontsize=14)
plt.show()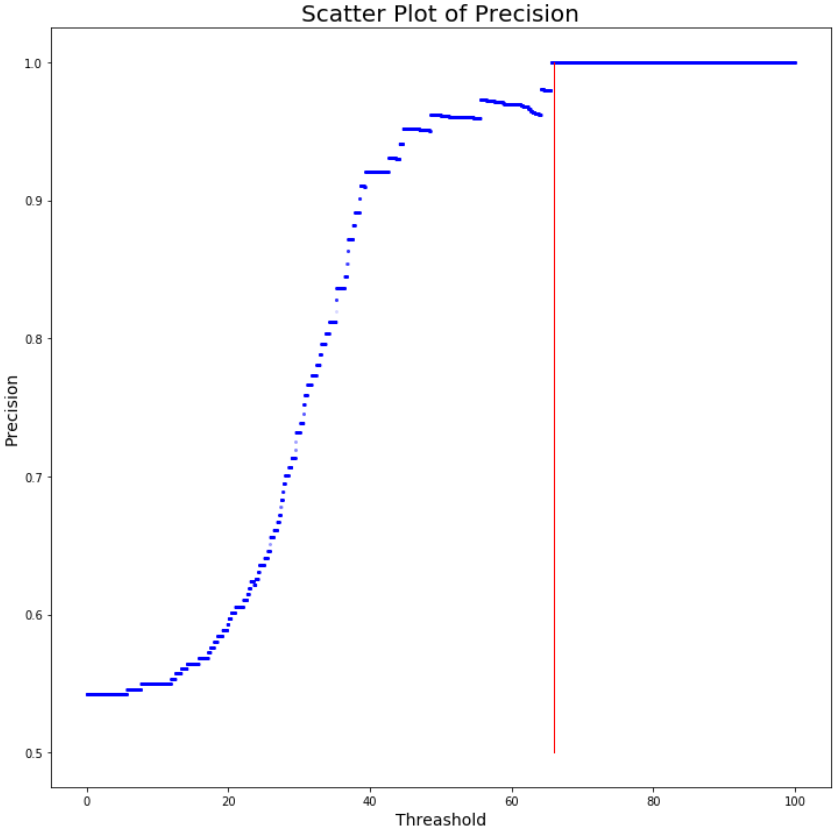
같은 구간의 값을 한 번 더 비교해 보자.
df_final2[['Threashold','Precision']][60000:67000:1000]
확인한 구간에서의 Precision이 전반적으로 떨어져 있다.
전체 구간에서 이런 차이가 발생할까?
#확률 합계를 1로 맞춰주지 않은 경우가 precision이 더 높은 경우
df_final2[df_final2['Precision']>df_final['Precision']]
# 15010 / 99999# precision이 비슷한 경우
df_final2[df_final2['Precision']==df_final['Precision']]
# 50802 / 99999#확률 합계를 1로 맞춰준 경우가 precision이 더 높은 경우
df_final2[df_final2['Precision']<df_final['Precision']]
# 34187 / 99999어떤 경우에 유의미한 차이가 있을까?
# 벌일 것 같다에 대한 예측값 전체 분포(확률값 합계를 1로 통일해 주기 전)
plt.hist(df_output_mutate[1])
#x 축 : output
#y 축 : 빈도
여기부터 축이 달라집니다.
x축이 Threashold(임계치), y 축이 빈도
plt.hist(df_final2[df_final2['Precision']>df_final['Precision']]['Threashold'])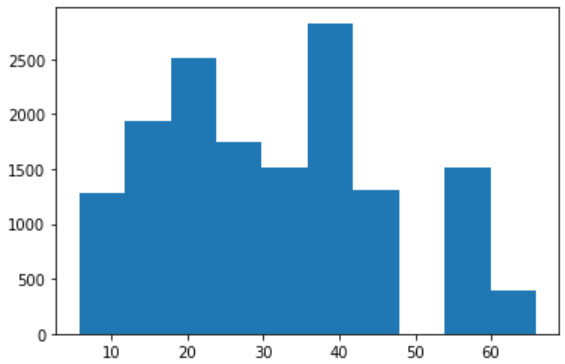
임게치를 50에 가까운 경우는 거의 전멸인 것을 볼 수 있다. (합계확률의 구성 비율이 50:50에 가까운 경우에 Precision이 극단적으로 떨어짐)
plt.hist(df_final2[df_final2['Precision']==df_final['Precision']]['Threashold'])
극단적인 값에는 예측률 차이가 크게 없다.
plt.hist(df_final2[df_final2['Precision']<df_final['Precision']]['Threashold'])
**임계치 50~60정도의 애매한 임계치의 경우 확률합계를 1로 맞춰주면 precision이 더 높아짐
위의 분포는 모델 및 데이터에 따라 달라질 수 있다. 또한 이런 경향을 다양한 상황에서 테스트 해 보지 않았음으로 일반화 하기에는 아직 이르다.
모델마다, 데이터 마다 해당 구간이 어디인지는 달라질 것인데, softmax 계열로 나온 값을 무작정 선형적으로 신뢰하긴 힘들수도 있을 것 같다.
다만 충분한 실험이 선행된다면, 애매한 구간에서의 확률합계를 1로 맞춰주는 작업의 유용성이 드러날 수 있을 것 같다.
또한 이 경우에서는 빈도 기준으로 확률합게를 1로 맞춰줄 시
합계1 미적용 시 우세 : 합계 1 적용시 우세 의 비율이 15010 : 34187 으로, 합계1 적용시의 우세 빈도가 2.27배정도 된다.
적용 여부와 무관한 경우까지 치면 65812 : 84989 로, 1.2배정도가 된다.


확률 합계를 1로 맞춰주는 행위가 '임계치에 따라 Precision이 역행하는 구간'에서의 보정효과가 있을 것으로 예상한다.
의료현장같은 높은 수준의 정밀도 혹은 민감도가 필요한 상황이라면 예측 output을 그대로 사용하기보다는 output을 전처리 해준 후, 해당 output의 변환값의 구간에 해당하는 정밀도와 민감도, 정확도를 함께 제공해야 정보를 받아들이는 사용자 입장에서의 수용도를 높일 수 있을 것이다.
모델 자체의 성능을 개선하지 않고도 Precision을 향상시킬 수 있을지도 모르겠다.
'반치용 > 기타 및 저장' 카테고리의 다른 글
| 단순 선형회귀 노트북 (0) | 2020.07.08 |
|---|---|
| [저장]딥러닝을 이용한 AR 앱 만들기 / keras - yolo v3 이용 (0) | 2020.06.25 |
| [기타] 이것들을 누가 보는걸까... (0) | 2020.06.18 |
| [파이썬]최단경로 알고리즘 (0) | 2020.06.18 |
| [파이썬]random matrix 만드는 코드 (0) | 2020.06.18 |

댓글